csp-201909

20190901（小明种苹果）

代码1

用struct AppleTree记录苹果树的相关信息，比如一开始的总苹果树，总共疏果的个数。苹果树编号从1开始

1
2
3
4
5
struct AppleTree{
    int id;
    int totNum;
    int shuguoNum;
}

有数据AppleTree trees[]。然后写一个cmp函数，对所有的AppleTree进行排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
//freopen("D://input.txt","r",stdin);
#include<bits/stdc++.h>
using namespace std;

struct AppleTree{
    int id, totNum, shuguoNum;
};
int n,m,T=0,k,p;
vector<AppleTree> trees;

bool cmp(AppleTree t1, AppleTree t2){
    if(t1.shuguoNum > t2.shuguoNum){
        return true;
    }else if(t1.shuguoNum == t2.shuguoNum){
        return t1.id < t2.id;
    }else{
        return false;
    }
}
int main(){
    //freopen("D://input.txt","r",stdin);
    ios::sync_with_stdio(false);
    cin>>n>>m;
    //init
    trees.resize(n);

    //input
    for(int i=0;i<n;i++){
        trees[i].id = i+1;
        cin>>trees[i].totNum;
        int a=0,b;
        for(int j=0;j<m;j++){
            cin>>b;
            a+=(-b);
        }
        trees[i].shuguoNum = a;
    }

    for(int i=0;i<n;i++){
        T+=(trees[i].totNum-trees[i].shuguoNum);
    }
    sort(trees.begin(),trees.end(),cmp);
    k = trees[0].id;
    p = trees[0].shuguoNum;

    //output
    cout<<T<<" "<<k<<" "<<p<<endl;

}

20190902（小明种苹果续）

代码1

我们设置一个结构体struct AppleTree来表示每个苹果树的id，一开始苹果树，疏果的个数，掉落的个数。

1
2
3
4
5
6
struct AppleTree{
    int id;
    int totNum;
    int shuguoNum;
    int dropNum = 0;
}

在第一次统计之后，以后每遇到疏果值，就累加shuguoNum，每遇到统计值a，就计算totNum-shuguoNum-dropNum-a，就得到当前的掉落的苹果个数，累加至dropNum。

如何计算相邻连续三棵苹果树发生苹果掉落情况的组数？int E，对于每个tree[i]，0<=i<=n-1，计算它前面的，它，它后面的是否都掉落了，若是，则累加组数E。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
//freopen("D://input.txt","r",stdin);
//ios::sync_with_stdio(false);
#include<bits/stdc++.h>
using namespace std;

struct AppleTree{
    int id, totNum, shuguoNum, dropNum; //shuguoNum,dropNum初始为0
};
int n,T=0,D=0,E=0;
vector<AppleTree> trees;

int main(){
    //freopen("D://input.txt","r",stdin);
    ios::sync_with_stdio(false);
    cin>>n;
    //init
    trees.resize(n);
    for(int i=0;i<n;i++){
        trees[i].id = i+1;
        trees[i].shuguoNum = trees[i].dropNum = 0;
    }

    //input
    for(int i=0;i<n;i++){
        int a;
        cin>>a;
        for(int j=0;j<a;j++){
            if(j==0){
                cin>>trees[i].totNum;
            }else{
                int b;
                cin>>b;
                if(b > 0){
                    trees[i].dropNum += (trees[i].totNum-trees[i].shuguoNum-trees[i].dropNum-b);
                }else{
                    trees[i].shuguoNum += (-b);
                }
            }
        }
    }

    for(int i=0;i<n;i++){
        T+=(trees[i].totNum-trees[i].shuguoNum-trees[i].dropNum);
        if(trees[i].dropNum > 0) D++;
        if(trees[(i==0?(n-1):(i-1))].dropNum>0 && trees[i].dropNum>0 && trees[(i+1)%n].dropNum>0){
            E++;
        }
    }

    //output
    cout<<T<<" "<<D<<" "<<E<<endl;
}

测试用例

1
2
3
4
5
4
4 74 -7 -12 -5
5 73 -8 -6 59 -4
5 76 -5 -10 60 -2
5 80 -6 -15 59 0

20190903（字符画）

代码1

我用array<int,3> picture[][] 来表示图画，用array<int,3> curBack 记录当前的背景颜色， 默认是0,0,0 。由于每一行有m/p个小区域，然后整个图画被分为n/q行，因此我要遍历m*n/(p*q)次，这样遍历：先遍历一行，看一个区域的颜色，若它的颜色跟当前的curBack相同，则直接输出空格，否则，更改终端的背景色（若颜色正好为黑色，则使用重置终端），然后输出空格，遍历了一行后，若与默认背景色不同，则重置终端，最后输出换行符。

对于输入，要判断三种情况：#abcd #abc #a

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
//freopen("D://input.txt","r",stdin);
//ios::sync_with_stdio(false);
#include<bits/stdc++.h>
using namespace std;
#define MAXM 1925
#define MAXN 1085

array<int,3> picture[MAXM][MAXN];
int m,n,p,q;
array<int,3> defBack = {0,0,0};

array<int,3> getColor(int xmin,int xmax,int ymin,int ymax){
    array<int,3> ans={0,0,0};
    for(int i=ymin;i<=ymax;i++){
        for(int j=xmin;j<=xmax;j++){
            ans[0]+=picture[i][j][0];
            ans[1]+=picture[i][j][1];
            ans[2]+=picture[i][j][2];
        }
    }
    int temp = p*q;
    ans[0] /= temp;
    ans[1] /= temp;
    ans[2] /= temp;
    return ans;
}

void printNum(int x){
    string str = to_string(x);
    for(int i=0;i<str.size();i++){
        printf("\\x%02X",str[i]);
    }
}
array<int,3> dealInput(char input[]){
    for(int i=0;i<strlen(input);i++){
        if(input[i]=='\n' || input[i]=='\0'){
            input[i]='\0';
            break;
        }
    }
    string str(input);
    if(strlen(input)==7){
        int a,b,c;
        sscanf(str.substr(1,2).c_str(),"%x",&a);
        sscanf(str.substr(3,2).c_str(),"%x",&b);
        sscanf(str.substr(5,2).c_str(),"%x",&c);
        return {a,b,c};
    }else if(strlen(input)==4){
        int a,b,c;
        string s;
        s = str.substr(1,1);
        s = s+s;
        sscanf(s.c_str(),"%x",&a);
        s = str.substr(2,1);
        s = s+s;
        sscanf(s.c_str(),"%x",&b);
        s = str.substr(3,1);
        s = s+s;
        sscanf(s.c_str(),"%x",&c);
        return {a,b,c};
    }else{
        int a;
        string s;
        s = str.substr(1,1);
        s = s+s;
        sscanf(s.c_str(),"%x",&a);
        return {a,a,a};
    }
}
int main(){
    //freopen("D://input.txt","r",stdin);
    //input
    scanf("%d%d\n%d%d\n",&m,&n,&p,&q);
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++){
            char input[10];
            fgets(input,10,stdin);
            picture[i][j] = dealInput(input);
        }
    }

    for(int i=0;i<n/q;i++){
        int ymin=i*q, ymax=i*q+q-1;
        array<int,3> curBack = {0,0,0};
        for(int j=0;j<m/p;j++){
            int xmin=j*p, xmax=j*p+p-1;
            array<int,3> color = getColor(xmin,xmax,ymin,ymax);
            if(color == curBack){
                printf("\\x%02X",' ');
            }else{
                if(color != defBack){
                    printf("\\x1B\\x%02X\\x%02X\\x%02X\\x%02X\\x%02X\\x%02X",'[','4','8',';','2',';');
                    printNum(color[0]);
                    printf("\\x%02X",';');
                    printNum(color[1]);
                    printf("\\x%02X",';');
                    printNum(color[2]);
                    printf("\\x%02X",'m');
                }else{
                    printf("\\x1B\\x%02X\\x%02X\\x%02X",'[','0','m');
                }
                printf("\\x%02X",' ');
            }
            curBack = color;
        }
        if(curBack != defBack){
            printf("\\x1B\\x%02X\\x%02X\\x%02X",'[','0','m');
        }
        printf("\\x%02X",'\n');
    }
}

//在输出每一行字符后，如果不是默认值，就设为默认值
//计算每个区域的坐标时弄错了，被q,n/q,p,m/p搞晕了
//输入函数对第二种情况的处理写错了

80分。

20190904（推荐系统）

代码1

设计一个结构体struct Commodity，表示商品，设有属性：商品的类别，商品编号，商品的得分。

1
2
3
4
5
struct Commodity{
    int type; //0..m-1
    int id;
    int score;
}

有一个set<Commodity> cmdSet ，存有每个商品的信息，显然需要指定比较函数，先按score，然后按照type，然后按照id。如果要删除或增加，只需要正常操作就好了。如果要查询，则用迭代器从头开始查，若某类商品已经选择够了，则跳到下一类商品继续查，直到达到了总的查询商品数或遍历完毕, 在这个过程中，保存商品类别到商品编号集合的映射， vector<set<int>> ans，不用map<int,vector<int>> ans的原因是，它较慢。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
//freopen("D://input.txt","r",stdin);
//ios::sync_with_stdio(false);
#include<bits/stdc++.h>
using namespace std;
#define MAXM 55

struct Commodity{
    int type; //0..m-1
    int id;
    int score;
    bool operator<(const Commodity c)const{
        if(score == c.score){
            if(type == c.type){
                return id<c.id;
            }
            return type<c.type;
        }else{
            return score>c.score;
        }
    }
    Commodity(int a,int b,int c){
        type=a;
        id=b;
        score=c;
    }
};
int m,n,opNum,k;
set<Commodity> cmdSet;
unordered_map<int,int> idToScore[MAXM];
int veck[MAXM];


vector<set<int>> ans;
void query(int k){
    //init
    for(int i=0;i<m;i++) ans[i].clear();

    set<Commodity>::iterator it = cmdSet.begin();
    while(k>0 && it!=cmdSet.end()){
        int type = (*it).type;
        if(veck[type] != 0){
            ans[type].insert((*it).id);
            k--;
            veck[type]--;
        }
        it++;
    }
}

int main(){
    //freopen("D://input.txt","r",stdin);
    scanf("%d%d",&m,&n);
    //init
    ans.resize(m);

    //input
    for(int i=0;i<n;i++){
        int id,score;
        scanf("%d%d",&id,&score);
        for(int j=0;j<m;j++){
            cmdSet.insert(Commodity(j,id,score));
            idToScore[j][id]=score;
        }
    }

    cin>>opNum;
    while(opNum--){
        int kind;
        scanf("%d",&kind);
        if(kind==1){
            int type,id,score;
            scanf("%d%d%d",&type,&id,&score);
            cmdSet.insert(Commodity(type,id,score));
            idToScore[type][id]=score;
        }else if(kind==2){
            int type,id;
            scanf("%d%d",&type,&id);
            cmdSet.erase(Commodity(type,id,idToScore[type][id]));
            idToScore[type].erase(id);
        }else{ //查询
            scanf("%d",&k);
            for(int i=0;i<m;i++) scanf("%d",&veck[i]);
            query(k);
            for(int i=0;i<m;i++){
                if(!ans[i].empty()){
                    set<int>::iterator it = ans[i].begin();
                    for(;it!=ans[i].end();it++){
                        printf("%d ",(*it));
                    }
                    printf("\n");
                }else{
                    printf("-1\n");
                }
            }
        }
    }
}

这个代码是通过的。我以前犯的错误是删除：我才用迭代的方式逐个去比较每个商品的type与id和给的type与id是否相同，然后删除，但是这样会很耗时，所以0分了，正确的做法是，对每个type建立id到score的映射，也就是unordered_map<int,int> idToScore[MAXM]，这样的话，可以使用函数cmdSet.erase(Commodity(type,id,score)) 来删除，效率更高。

20190905（城市规划）

代码1

设置一个邻接表vector<vector<int>> dis 表示相邻两个点之间的最短路径，当然一开始只有直接相连的两个点的最短距离，之后可以用floyd算法算出每两个点之间的最短距离。设置一个vector<int> imp 表示重要的点的集合，然后不断选出K个点，计算它们的两两之间距离总和。

关于如何选出K个点，可以使用递归的方式。

具体如何写递归，可以看代码具体实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
//freopen("D://input.txt","r",stdin);
//ios::sync_with_stdio(false);
#include<bits/stdc++.h>
using namespace std;
#define INF 1e18

int n,m,k;
vector<vector<long long>> dis;
vector<int> imp;

void floyd(){
    for(int k=1;k<=n;k++){
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                if(dis[i][k]!=INF && dis[k][j]!=INF && dis[i][k]+dis[k][j]<dis[i][j]){
                    dis[i][j] = dis[i][k]+dis[k][j];
                }
            }
        }
    }
}

long long minSum = INF;
vector<int> veck; //保存那选出来的k个地点
long long computeSum(){
    long long temp=0;
    for(int i=0;i<k;i++){
        for(int j=i+1;j<k;j++){
            temp+=dis[veck[i]][veck[j]];
        }
    }
    return temp;
}
//从imp[beg,ed]中找x个
void getK(int beg,int ed,int x){
    if(ed-beg+1==x){
        for(int i=beg;i<=ed;i++){
            veck.push_back(imp[i]);
        }
        long long temp = computeSum();
        if(temp<minSum) minSum=temp;
        for(int i=beg;i<=ed;i++){
            veck.pop_back();
        }
        return;
    }else if(x==0){
        long long temp = computeSum();
        if(temp<minSum) minSum=temp;
        return;
    }
    getK(beg,ed-1,x);
    veck.push_back(imp[ed]);
    getK(beg,ed-1,x-1);
    veck.pop_back();
}
int main(){
    //freopen("D://input.txt","r",stdin);
    scanf("%d%d%d",&n,&m,&k);
    //init
    dis.resize(n+1);
    for(int i=0;i<n+1;i++){
        dis[i].resize(n+1);
        for(int j=0;j<n+1;j++){
            if(i==j) dis[i][j]=0;
            else dis[i][j] = INF;
        }
    }
    imp.resize(m);

    //input
    int a,b,c;
    for(int i=0;i<m;i++){
        scanf("%d",&a);
        imp[i]=a;
    }
    for(int i=0;i<n-1;i++){
        scanf("%d%d%d",&a,&b,&c);
        dis[a][b]=dis[b][a]=c;
    }

    floyd();
    getK(0,m-1,k);

    //output
    cout<<minSum<<endl;
}

0分。超时

代码2

但是floyd算法太慢了，由于这个题本身考虑的是树，所以可以用每个点的BFS来求最短路径，把floyd算法替换掉。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
//freopen("D://input.txt","r",stdin);
//ios::sync_with_stdio(false);
#include<bits/stdc++.h>
using namespace std;
#define INF 1e18

int n,m,k;
vector<vector<long long>> dis;
vector<int> imp;

struct Node{
    int v;
    long long dist;
};

void computeShortestDist(){
    for(int i=1;i<=n;i++){
        //init
        vector<bool> vis(n+1);
        for(int i=1;i<=n;i++) vis[i]=false;

        Node node = {i,0};
        queue<Node> q;
        q.push(node);
        vis[i] = true;
        while(!q.empty()){
            node = q.front();
            q.pop();
            for(int j=1;j<=n;j++){
                if(dis[node.v][j] != INF && node.v!=j && vis[j]==false){
                    dis[i][j] = node.dist + dis[node.v][j];
                    q.push({j,dis[i][j]});
                    vis[j] = true;
                }
            }
        }
    }
}

long long minSum = INF;
vector<int> veck; //保存那选出来的k个地点
long long computeSum(){
    long long temp=0;
    for(int i=0;i<k;i++){
        for(int j=i+1;j<k;j++){
            temp+=dis[veck[i]][veck[j]];
        }
    }
    return temp;
}
//从imp[beg,ed]中找x个
void getK(int beg,int ed,int x){
    if(ed-beg+1==x){
        for(int i=beg;i<=ed;i++){
            veck.push_back(imp[i]);
        }
        long long temp = computeSum();
        if(temp<minSum) minSum=temp;
        for(int i=beg;i<=ed;i++){
            veck.pop_back();
        }
        return;
    }else if(x==0){
        long long temp = computeSum();
        if(temp<minSum) minSum=temp;
        return;
    }
    getK(beg,ed-1,x);
    veck.push_back(imp[ed]);
    getK(beg,ed-1,x-1);
    veck.pop_back();
}
int main(){
    //freopen("D://input.txt","r",stdin);
    scanf("%d%d%d",&n,&m,&k);
    //init
    dis.resize(n+1);
    for(int i=0;i<n+1;i++){
        dis[i].resize(n+1);
        for(int j=0;j<n+1;j++){
            if(i==j){
                dis[i][j]=0;
            }
            else {
                dis[i][j] = INF;
            }
        }
    }
    imp.resize(m);

    //input
    int a,b,c;
    for(int i=0;i<m;i++){
        scanf("%d",&a);
        imp[i]=a;
    }
    for(int i=0;i<n-1;i++){
        scanf("%d%d%d",&a,&b,&c);
        dis[a][b]=dis[b][a]=c;
    }

    computeShortestDist();
    getK(0,m-1,k);

    //output
    cout<<minSum<<endl;
}

0分。还是超时。

代码3

这题采用动态规划的方法，但是这个动态规划是最难的。dp[i][j] 表示以i为根节点的子树中选j个重要节点时，这个子树内选中的重要节点的两两距离之和，再加上，子树内j个重要节点到达剩余K-j个重要节点需要经过的子树内路径的长度之和。

1

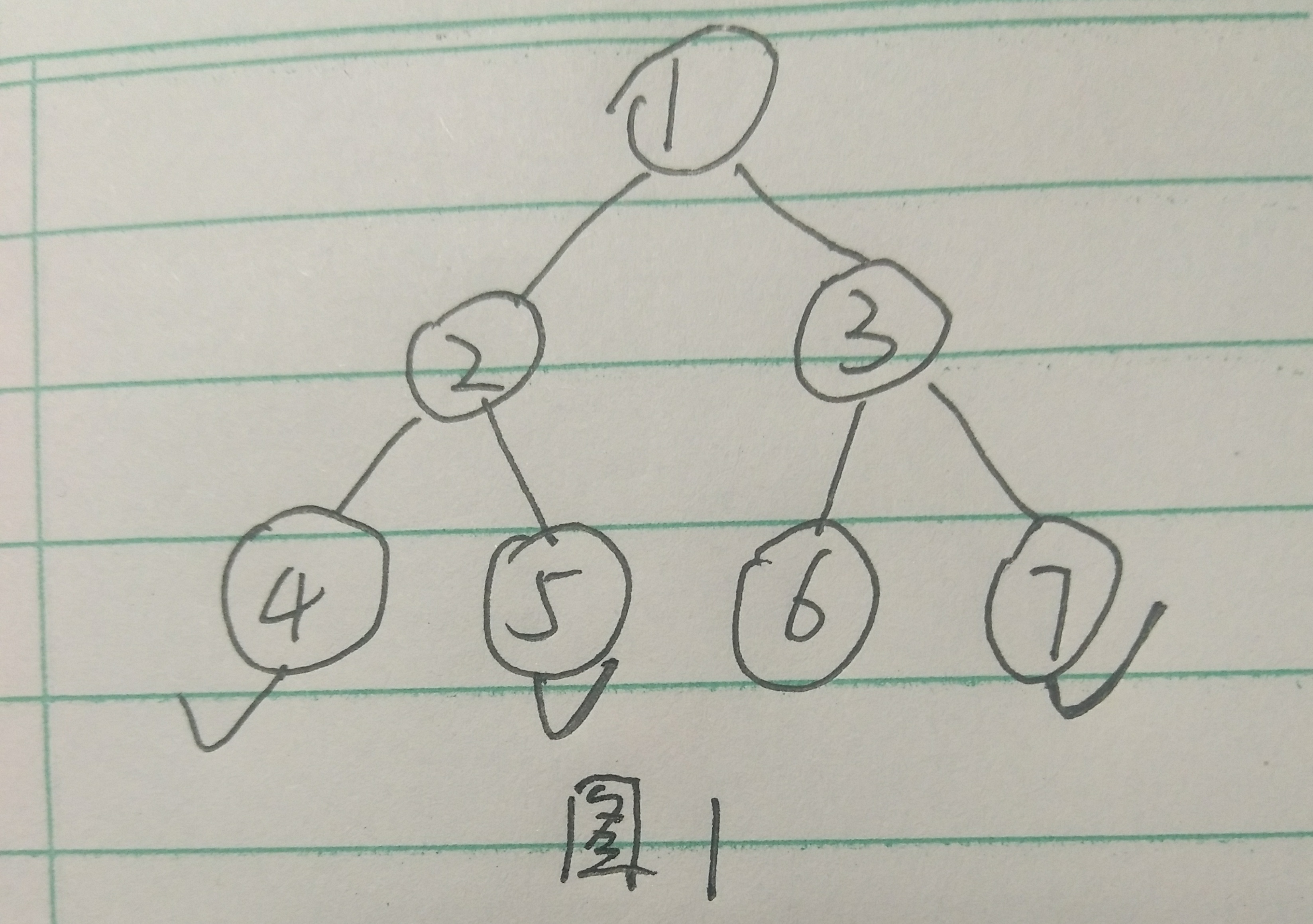
例如图1，要选出3个重要节点。在1子树中，dp[1][2] = 2+2+2，(注意，这里的dp[1][2]没有计算完，只是中间值，后面还要考虑(3,6,7)部分才能得到最终解)，第一个2表示4和5之间的距离，第二个2表示4为了到达剩余的3-2=1个重要节点所需要经过的<4,2,1>这个1子树内路径的长度之和，也就是1=<4,2,1>的长度 (3-2)；对于第三个2，表示5为了到达剩余的3-2个重要节点所需要经过的<5,2,1>这个1子树内路径的长度之和，也就是1=<5,2,1>的长度 (3-2)。

但是如何用递推的方式求dp[i][j] 呢。对于图1的2子树，dp[2]的计算由它的子树4和5的dp计算而来。dp[i]初始为{0, -1, -1}，表示i子树选中0个重要节点时，dp值为0，选中1个和2个重要节点时，dp值为-1，也就是表示2子树内选择不出这么多的重要节点。下面是计算过程的样例。

  1. 计算dp[4]为{0, 0, -1}
  2. 更新dp[2]为{0, 2, -1}, 这个结果是(2,4)部分的dp[2]的结果。
  3. 计算机dp[4]为{0, 0, -1}
  4. 更新dp[2]为{0, 2, 4}，这时，要合并(2,4)部分和(5)部分。(2,4)部分有1个选中的重要节点，(5)部分有1个选中的重要节点，因此(2,4,5)可以有2个选中的重要节点，dp[2][2] = dp[2][1] + dp[5][1] + 2。2代表5到达另外两个重要节点，所要经过的2次<5,2>路径的长度之和。dp[2][1]=0+1+1，dp[5][1]=0，所以dp[2][2] = 0+1+1+0+1+1，第1个1和第3个1组成2，表示4和5之间的距离，第2个1表示4到达另外一个重要节点要经过的<4,2>路径长度，第4个1表示5到达另外一个重要节点要经过的<5,2>路径长度。

还有一个问题，要更新dp[i]时，从dp[i][k]更新到dp[i][1] 还是从dp[i][1] 更新到dp[i][k]。答案是前者，如果要用后者，可以开一个dp2，然后计算完成后，把dp2赋值到dp就好了。

还有一个情况，万一2子树的根节点2就是重要节点呢？我们之前的计算只考虑2子树的子树的重要节点情况对于2子树的影响，但是没有考虑2节点本身。假如2子树的子树有2个重要节点，那么2子树的dp[2][2]可以为选择2节点和子树中的1个节点组成的2个选中的重要节点，说不定这种情况就比选择2子树的子树中的2个重要节点的情况要好。而且，2子树也可以有选择3个重要节点的情况，也就是子树中的2个加上2节点的1个。

还有就是最优性原理的证明。dp[i][j]的j个重要节点是来自不同的子树的，那么不同的情况选出不同的dp[i][j] 的值，当然最小的那个就是最优的，假如后面的最优决策中用到了这个dp[i][j]，那么是否说明这个dp[i][j]就是最优的？是的。为什么？因为dp[i1][j1] = dp[i][j] + dp[i1][j2] + num 这个公式是进行推导dp的递推式，假如后面的决策最优，那么dp[i][j]也最优。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <iostream>
#include <vector>
using namespace std;

int N, M, K;
vector<bool> imp;
vector<vector<pair<int, int>>> tree;
vector<vector<long long>> dp; 

void solve(int u, int fa) {
    vector<long long>& cur = dp[u];        // 当前要求解的数组
    cur[0] = 0;                            // j = 0(一个重要节点都不选)时，路径和显然为0
    for (const auto& pr: tree[u]) if (pr.first != fa) {
        solve(pr.first, u);                // 先解出子问题dp[pr.first]，然后合并，分治思想
        vector<long long>& sub = dp[pr.first];
        for (int x = K; x > 0; --x) {      // 合并时，重用了数组cur。应该将此时的cur视为前n-1个子树合并后的结果
            for (int y = x; y >= 0; --y) {
                if (cur[y] != -1 && sub[x - y] != -1) {
                    long long t = cur[y] + sub[x - y] + (long long)pr.second * (x - y) * (K - x + y);
                    if (cur[x] == -1 || cur[x] > t) cur[x] = t;
                }
            }
        }
    }
    if (imp[u]) {
        for (int i = K; i > 0; --i)
            if (cur[i] == -1 || cur[i] > cur[i - 1]) // cur[i] != -1的话，cur[i-1]不可能等于-1
                cur[i] = cur[i - 1];
    }
}

int main() {
    cin.tie(nullptr);
    ios_base::sync_with_stdio(false);
    cin >> N >> M >> K;
    imp.resize(N + 1);
    for (int i = 0; i < M; ++i) {
        int x;
        cin >> x;
        imp[x] = true;
    }
    tree.resize(N + 1);
    for (int i = 1; i < N; ++i) {
        int a, b, c;
        cin >> a >> b >> c;
        tree[a].emplace_back(b, c);
        tree[b].emplace_back(a, c);
    }
    dp.resize(N + 1, vector<long long>(K + 1, -1));
    solve(1, 0);
    cout << dp[1][K] << endl;
    return 0;
}
赏

谢谢你请我吃糖果

扫一扫，分享到微信

微信分享二维码

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

很惭愧<br><br>只做了一点微小的工作<br>谢谢大家